Maple
Powerful math software that is easy to use
• Maple for Academics • Maple for Students • Maple Learn • Maple Calculator App • Maple for Industry and Government • Maple Flow • Maple for Individuals
The Lotka|Volterra equations, also known as the predator|prey equations, are a pair of first-order, nonlinear, differential equations frequently used to describe the dynamics of biological systems in which two species interact, one as a predator and the other as prey. The populations change through time according to the pair of equations:
where
and 
represent the growth rates of the two populations over time;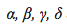
are positive real parameters describing the interaction of the two species.The Lotka|Volterra system of equations is an example of a Kolmogorov model, which is a more general framework that can model the dynamics of ecological systems with predator|prey interactions, competition, disease, and mutualism.1
Maple is powerful math software that makes it easy to learn about Lotka-Volterra equations, and to analyze, explore, visualize, and solve mathematical problems from virtually every branch of mathematics. Student pricing available.
1 Source: Wikipedia
